192. Searching + Traversal Introduction
We do searching everyday. It is part of our lives..
Searching/Traversal
- Linear Search: O(n)
- Binary Search: O(log n)
- Depth First Search
- Breadth First Search
193. Linear Search
In CS, Linear search is the method of finding target values in a list. It is sequential work.
ex) [6, 2, 3, 13, 9]
best case: O(1) ex) 6
worst case : O(n) ex) 9
But you can not use this for huge database such as google search..
| var arr = ['a', 'b', 'c', 'd']; console.log(arr.indexOf('c')) console.log(arr.findIndex(item => item === 'c')) console.log(arr.find(item => item === 'c')) console.log(arr.includes('c')) 2 2 c true |
Is there a better way?
194. Binary Search
Just go in the middle and choose whether to go left or right. Carry on.
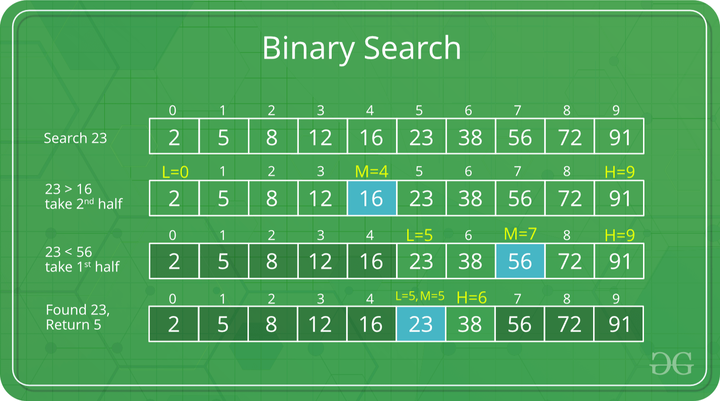
Searching through tree structure gives better performance than just traversing all the lists.
195. Graph + Tree Traversals
We used loop to travel all the data structure.
Graph Traversal
- BFS(Breadth First Search)
- DFS(Depth First Search)
Tree Traversal
- BFS(Breadth First Search)
- DFS(Depth First Search)
Why we don’t store simply in list?
- Because we get O log n, instead of O(n) of arrays
- Trees and Graphs are very fit to various data structures.
196. BFS Introduction
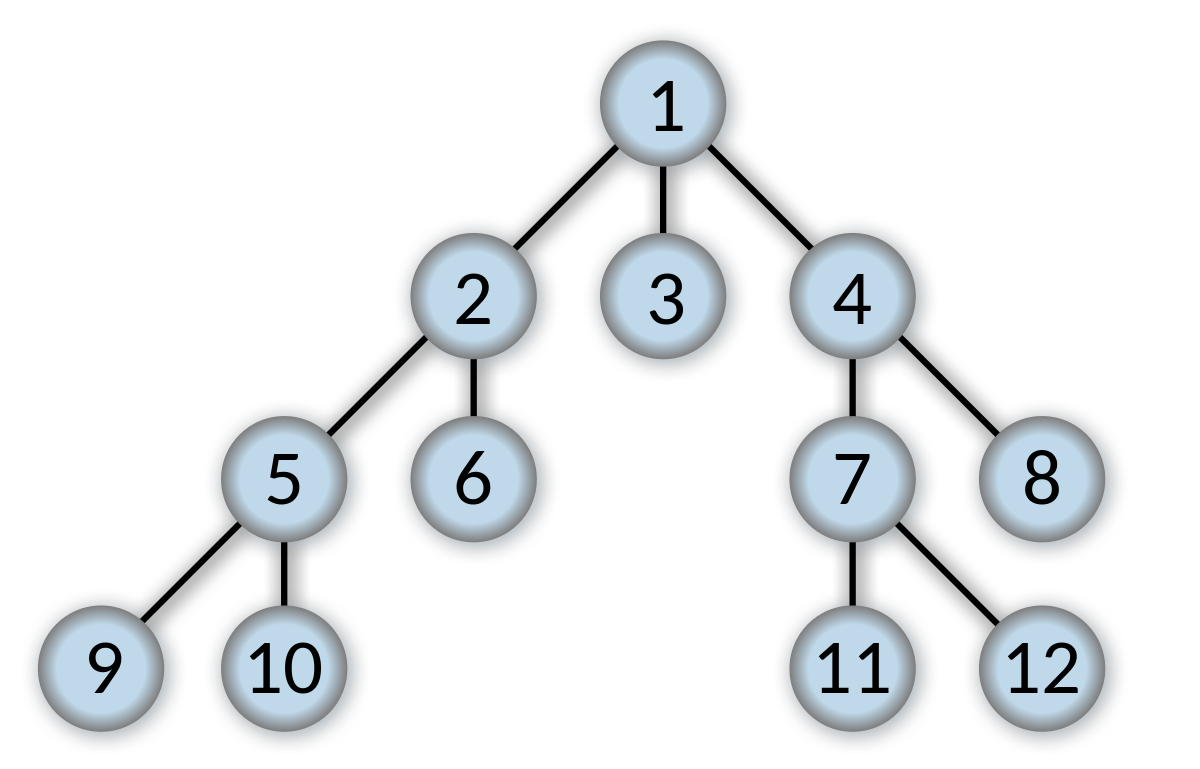
BFS stands for Breadth First Search.
You start from the root, and both left and right in next level, and also left and right in next level, and so on. Simply you visit nodes layer by layer.
It requires additional memory to track all nodes and its children. Because when you are in 4th turn, you still have to remember what’s under 2 and 3 in order to go back after 4th.
197. DFS Introduction
DFS requires less memory load than BFS because you don’t need to store all the child pointers to each other.
Depth is the first priority. DFS search as deep as possible.

198. BFS vs DFS
BFS
- pros
- cons
When It’s good?
If you have additional node’s location info and it is located in upper level of tree or a graph, BFS is better.
DFS
- pros
- cons
199. Resources: BFS vs DFS
201. Interview Question
//If you know a solution is not far from the root of the tree:
-> BFS.
//If the tree is very deep and solutions are rare:
-> BFS. Because DFS will take long time in deep level
//If the tree is very wide:
-> DFS. Because BFS will need too much memory
//If solutions are frequent but located deep in the tree:
-> DFS.
//Determining whether a path exists between two nodes:
-> DFS.
//Finding the shortest path:
-> BFS.
202. breadthFirstSearch
| class Node { constructor(value){ this.left = null; this.right = null; this.value = value; } } class BinarySearchTree { constructor(){ this.root = null; } insert(value){ const newNode = new Node(value); if (this.root === null) { this.root = newNode; } else { let currentNode = this.root; while(true){ if(value < currentNode.value){ //Left if(!currentNode.left){ currentNode.left = newNode; return this; } currentNode = currentNode.left; } else { //Right if(!currentNode.right){ currentNode.right = newNode; return this; } currentNode = currentNode.right; } } } } lookup(value){ if (!this.root) { return false; } let currentNode = this.root; while(currentNode){ if(value < currentNode.value){ currentNode = currentNode.left; } else if(value > currentNode.value){ currentNode = currentNode.right; } else if (currentNode.value === value) { return currentNode; } } return null } remove(value) { if (!this.root) { return false; } let currentNode = this.root; let parentNode = null; while(currentNode){ if(value < currentNode.value){ parentNode = currentNode; currentNode = currentNode.left; } else if(value > currentNode.value){ parentNode = currentNode; currentNode = currentNode.right; } else if (currentNode.value === value) { //We have a match, get to work! //Option 1: No right child: if (currentNode.right === null) { if (parentNode === null) { this.root = currentNode.left; } else { //if parent > current value, make current left child a child of parent if(currentNode.value < parentNode.value) { parentNode.left = currentNode.left; //if parent < current value, make left child a right child of parent } else if(currentNode.value > parentNode.value) { parentNode.right = currentNode.left; } } //Option 2: Right child which doesnt have a left child } else if (currentNode.right.left === null) { currentNode.right.left = currentNode.left; if(parentNode === null) { this.root = currentNode.right; } else { //if parent > current, make right child of the left the parent if(currentNode.value < parentNode.value) { parentNode.left = currentNode.right; //if parent < current, make right child a right child of the parent } else if (currentNode.value > parentNode.value) { parentNode.right = currentNode.right; } } //Option 3: Right child that has a left child } else { //find the Right child's left most child let leftmost = currentNode.right.left; let leftmostParent = currentNode.right; while(leftmost.left !== null) { leftmostParent = leftmost; leftmost = leftmost.left; } //Parent's left subtree is now leftmost's right subtree leftmostParent.left = leftmost.right; leftmost.left = currentNode.left; leftmost.right = currentNode.right; if(parentNode === null) { this.root = leftmost; } else { if(currentNode.value < parentNode.value) { parentNode.left = leftmost; } else if(currentNode.value > parentNode.value) { parentNode.right = leftmost; } } } return true; } } } breadthFirstSearch() { let currentNode = this.root; let list = []; // order of breadthFirstSearch // This queue can be really large if you search very wide tree let queue = []; queue.push(currentNode); while(queue.length > 0) { currentNode = queue.shift(); console.log(currentNode.value) list.push(currentNode.value); if (currentNode.left) { queue.push(currentNode.left); } if (currentNode.right) { queue.push(currentNode.right); } } return list; } } const tree = new BinarySearchTree(); tree.insert(9) tree.insert(4) tree.insert(6) tree.insert(20) tree.insert(170) tree.insert(15) tree.insert(1) console.log(tree.breadthFirstSearch()); // 9 // 4 20 //1 6 15 170 function traverse(node) { const tree = { value: node.value }; tree.left = node.left === null ? null : traverse(node.left); tree.right = node.right === null ? null : traverse(node.right); return tree; } |
203. breadthFirstSearchRecursive()
| class Node { constructor(value){ this.left = null; this.right = null; this.value = value; } } class BinarySearchTree { constructor(){ this.root = null; } insert(value){ const newNode = new Node(value); if (this.root === null) { this.root = newNode; } else { let currentNode = this.root; while(true){ if(value < currentNode.value){ //Left if(!currentNode.left){ currentNode.left = newNode; return this; } currentNode = currentNode.left; } else { //Right if(!currentNode.right){ currentNode.right = newNode; return this; } currentNode = currentNode.right; } } } } lookup(value){ if (!this.root) { return false; } let currentNode = this.root; while(currentNode){ if(value < currentNode.value){ currentNode = currentNode.left; } else if(value > currentNode.value){ currentNode = currentNode.right; } else if (currentNode.value === value) { return currentNode; } } return null } remove(value) { if (!this.root) { return false; } let currentNode = this.root; let parentNode = null; while(currentNode){ if(value < currentNode.value){ parentNode = currentNode; currentNode = currentNode.left; } else if(value > currentNode.value){ parentNode = currentNode; currentNode = currentNode.right; } else if (currentNode.value === value) { //We have a match, get to work! //Option 1: No right child: if (currentNode.right === null) { if (parentNode === null) { this.root = currentNode.left; } else { //if parent > current value, make current left child a child of parent if(currentNode.value < parentNode.value) { parentNode.left = currentNode.left; //if parent < current value, make left child a right child of parent } else if(currentNode.value > parentNode.value) { parentNode.right = currentNode.left; } } //Option 2: Right child which doesnt have a left child } else if (currentNode.right.left === null) { if(parentNode === null) { this.root = currentNode.left; } else { currentNode.right.left = currentNode.left; //if parent > current, make right child of the left the parent if(currentNode.value < parentNode.value) { parentNode.left = currentNode.right; //if parent < current, make right child a right child of the parent } else if (currentNode.value > parentNode.value) { parentNode.right = currentNode.right; } } //Option 3: Right child that has a left child } else { //find the Right child's left most child let leftmost = currentNode.right.left; let leftmostParent = currentNode.right; while(leftmost.left !== null) { leftmostParent = leftmost; leftmost = leftmost.left; } //Parent's left subtree is now leftmost's right subtree leftmostParent.left = leftmost.right; leftmost.left = currentNode.left; leftmost.right = currentNode.right; if(parentNode === null) { this.root = leftmost; } else { if(currentNode.value < parentNode.value) { parentNode.left = leftmost; } else if(currentNode.value > parentNode.value) { parentNode.right = leftmost; } } } return true; } } } BreadthFirstSearch(){ let currentNode = this.root; let list = []; let queue = []; queue.push(currentNode); while(queue.length > 0){ currentNode = queue.shift(); list.push(currentNode.value); if(currentNode.left) { queue.push(currentNode.left); } if(currentNode.right) { queue.push(currentNode.right); } } return list; } BreadthFirstSearchR(queue, list) { if (!queue.length) { return list; } const currentNode = queue.shift(); list.push(currentNode.value); if (currentNode.left) { queue.push(currentNode.left); } if (currentNode.right) { queue.push(currentNode.right); } return this.BreadthFirstSearchR(queue, list); } } const tree = new BinarySearchTree(); tree.insert(9) tree.insert(4) tree.insert(6) tree.insert(20) tree.insert(170) tree.insert(15) tree.insert(1) console.log('BFS', tree.BreadthFirstSearch()); console.log('BFS', tree.BreadthFirstSearchR([tree.root], [])) // 9 // 4 20 //1 6 15 170 function traverse(node) { const tree = { value: node.value }; tree.left = node.left === null ? null : traverse(node.left); tree.right = node.right === null ? null : traverse(node.right); return tree; } |
204. PreOrder, InOrder, PostOrder
DFS depthFirstSearch
There are 3 types of order in DFS.
// 101
// 33 105
in order: 33, 101, 105
preorder: 101, 33, 105
postorder: 33, 105, 101
// 9
// 4 20
// 1 6 15 170
in order: [1, 4, 6, 9, 15, 20, 170] - 숫자 크기대로
preorder: [9, 4, 1, 6, 20, 15, 170] - parent node에서 먼저 시작한다. 왜 이걸 쓰는가? tree를 다시 만드는데 굉장히 유용한 방식.
postorder: [1, 6, 4, 15, 170, 20, 9] - 가장 아래로 내려가서 루트로 올라가는 방식
205. depthFirstSearch
| class Node { constructor(value){ this.left = null; this.right = null; this.value = value; } } class BinarySearchTree { constructor(){ this.root = null; } insert(value){ const newNode = new Node(value); if (this.root === null) { this.root = newNode; } else { let currentNode = this.root; while(true){ if(value < currentNode.value){ //Left if(!currentNode.left){ currentNode.left = newNode; return this; } currentNode = currentNode.left; } else { //Right if(!currentNode.right){ currentNode.right = newNode; return this; } currentNode = currentNode.right; } } } } lookup(value){ if (!this.root) { return false; } let currentNode = this.root; while(currentNode){ if(value < currentNode.value){ currentNode = currentNode.left; } else if(value > currentNode.value){ currentNode = currentNode.right; } else if (currentNode.value === value) { return currentNode; } } return null } remove(value) { if (!this.root) { return false; } let currentNode = this.root; let parentNode = null; while(currentNode){ if(value < currentNode.value){ parentNode = currentNode; currentNode = currentNode.left; } else if(value > currentNode.value){ parentNode = currentNode; currentNode = currentNode.right; } else if (currentNode.value === value) { //We have a match, get to work! //Option 1: No right child: if (currentNode.right === null) { if (parentNode === null) { this.root = currentNode.left; } else { //if parent > current value, make current left child a child of parent if(currentNode.value < parentNode.value) { parentNode.left = currentNode.left; //if parent < current value, make left child a right child of parent } else if(currentNode.value > parentNode.value) { parentNode.right = currentNode.left; } } //Option 2: Right child which doesnt have a left child } else if (currentNode.right.left === null) { if(parentNode === null) { this.root = currentNode.left; } else { currentNode.right.left = currentNode.left; //if parent > current, make right child of the left the parent if(currentNode.value < parentNode.value) { parentNode.left = currentNode.right; //if parent < current, make right child a right child of the parent } else if (currentNode.value > parentNode.value) { parentNode.right = currentNode.right; } } //Option 3: Right child that has a left child } else { //find the Right child's left most child let leftmost = currentNode.right.left; let leftmostParent = currentNode.right; while(leftmost.left !== null) { leftmostParent = leftmost; leftmost = leftmost.left; } //Parent's left subtree is now leftmost's right subtree leftmostParent.left = leftmost.right; leftmost.left = currentNode.left; leftmost.right = currentNode.right; if(parentNode === null) { this.root = leftmost; } else { if(currentNode.value < parentNode.value) { parentNode.left = leftmost; } else if(currentNode.value > parentNode.value) { parentNode.right = leftmost; } } } return true; } } } BreadthFirstSearch(){ let currentNode = this.root; let list = []; let queue = []; queue.push(currentNode); while(queue.length > 0){ currentNode = queue.shift(); list.push(currentNode.value); if(currentNode.left) { queue.push(currentNode.left); } if(currentNode.right) { queue.push(currentNode.right); } } return list; } BreadthFirstSearchR(queue, list) { if (!queue.length) { return list; } const currentNode = queue.shift(); list.push(currentNode.value); if (currentNode.left) { queue.push(currentNode.left); } if (currentNode.right) { queue.push(currentNode.right); } return this.BreadthFirstSearchR(queue, list); } DFTPreOrder(currentNode, list) { return traversePreOrder(this.root, []); } DFTPostOrder(){ return traversePostOrder(this.root, []); } DFTInOrder(){ return traverseInOrder(this.root, []); } } function traversePreOrder(node, list){ list.push(node.value); if(node.left) { traversePreOrder(node.left, list); } if(node.right) { traversePreOrder(node.right, list); } return list; } function traverseInOrder(node, list){ if(node.left) { traverseInOrder(node.left, list); } list.push(node.value); if(node.right) { traverseInOrder(node.right, list); } return list; } function traversePostOrder(node, list){ if(node.left) { traversePostOrder(node.left, list); } if(node.right) { traversePostOrder(node.right, list); } list.push(node.value); return list; } const tree = new BinarySearchTree(); tree.insert(9) tree.insert(4) tree.insert(6) tree.insert(20) tree.insert(170) tree.insert(15) tree.insert(1) // tree.remove(170); // JSON.stringify(traverse(tree.root)) console.log('BFS', tree.BreadthFirstSearch()); console.log('BFS', tree.BreadthFirstSearchR([tree.root], [])) console.log('DFSpre', tree.DFTPreOrder()); console.log('DFSin', tree.DFTInOrder()); console.log('DFSpost', tree.DFTPostOrder()); // 9 // 4 20 //1 6 15 170 function traverse(node) { const tree = { value: node.value }; tree.left = node.left === null ? null : traverse(node.left); tree.right = node.right === null ? null : traverse(node.right); return tree; } |
https://leetcode.com/problems/validate-binary-search-tree/
https://visualgo.net/en/dfsbfs?slide=1
207. Graph Traversals
in Graph Traversals,
Breadth First Search is good for shortest path. What’s the closest connection in Facebook for e.g.
Deep First Search is good to check something if it exists
208. BFS in Graphs
https://visualgo.net/en/dfsbfs
BFS enables to conver graph into tree. which node is parent and childs?
pros
- shortest path
- closer nodes
cons
- more memory to remember which one is parents and children nodes
209. DFS in Graphs
Maze puzzle
DFS method is exactly same with solving maze problem.
Pros
- less memory
- Good to check if it does Path exist?
Cons
- Can get slow
210. Dijkstra + Bellman-Ford Algorithms
BFS is great for shortest path problem but DFS, BFS doesn’t really care about the weight of the edge. edge의 weight를 모두 같다고 고려하기 때문에 BFS, DFS는 이 경우에는 부적절.
Shortest path problems for considering weight of edges
- Dijkstra: faster than bellman-ford. But impossible to consider negative weight
- Bellman-Ford: complexity is a bit high.
Dijkstra, Bellman-Ford는 edge의 weight를 고려했을 때 가장 빠른 길을 찾는 알고리즘이다. 구글 맵스에서 가장 빠른 길을 찾아준다.
Weight가 음수일 경우 Bellman-Ford를 쓰고, 양수일 경우 Dijkstra를 써야한다. 퍼포먼스 자체는 Dijkstra가 더 좋다.
211. Searching + Traversal Review
Linear Search : can be good. But not best option due to O(n)
Binary Search : O(log n)
Depth First Search : go as deep as possible
Breadth First Search : traversing level by level
'Research > Data structure & algorithm' 카테고리의 다른 글
| 01. Array 배열의 정의와 구현(JS) (0) | 2023.02.05 |
|---|---|
| s15. Algorithm: Dynamic Programming (0) | 2022.12.03 |
| s12. Algorithm: Recursion (0) | 2022.12.01 |
| s11. Data Structure: Graphs (0) | 2022.11.30 |
| s10. Data Structure: Trees (0) | 2022.11.29 |



댓글