Background
Data Structure + Algorithms = Programs
Class {} + function() = Programs
What is Algorithms?
Algorithms are steps in a process that we take to perform a desired action with computers
https://en.wikipedia.org/wiki/List_of_algorithms
Why important?
Certain algorithms make simplify BigO complexity such as O(2^n) -> O(n)
154. Recursion Introduction
Background
Recursion is more like a concept not an algorithm.
Common topic for interview.
What is Recursion
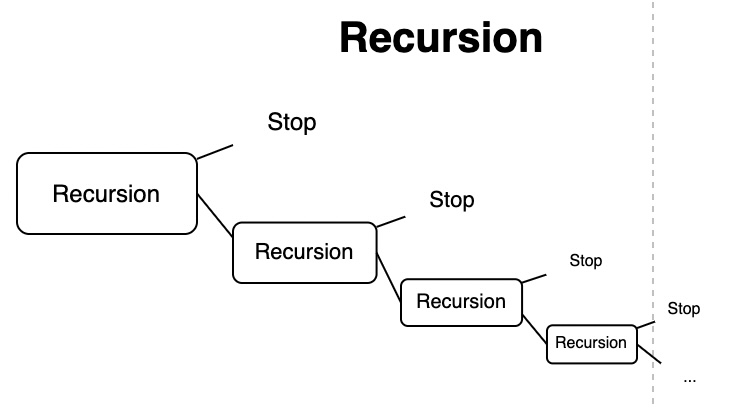
Recursion is when you defined something in terms of itself. such as the function that refers itself inside the function.
Linux
| ls ls -R |
With -R that stands for recursive, you can get all the file list below the current directory.
| function inception() { inception(); } |
What is good?
Recursion is good for solving tasks that have repeated subtasks to do.
For example
- traversing in Searching, Sorting.
- DOM traversing
155. Stack Overflow
Problems of Recursion
- hard to understand
- calling function over and over -> stack overflow
구글 브라우저에서 inception() 디버깅해서 콜스택 확인하기
| function inception() { debugger; inception(); } inception(); |
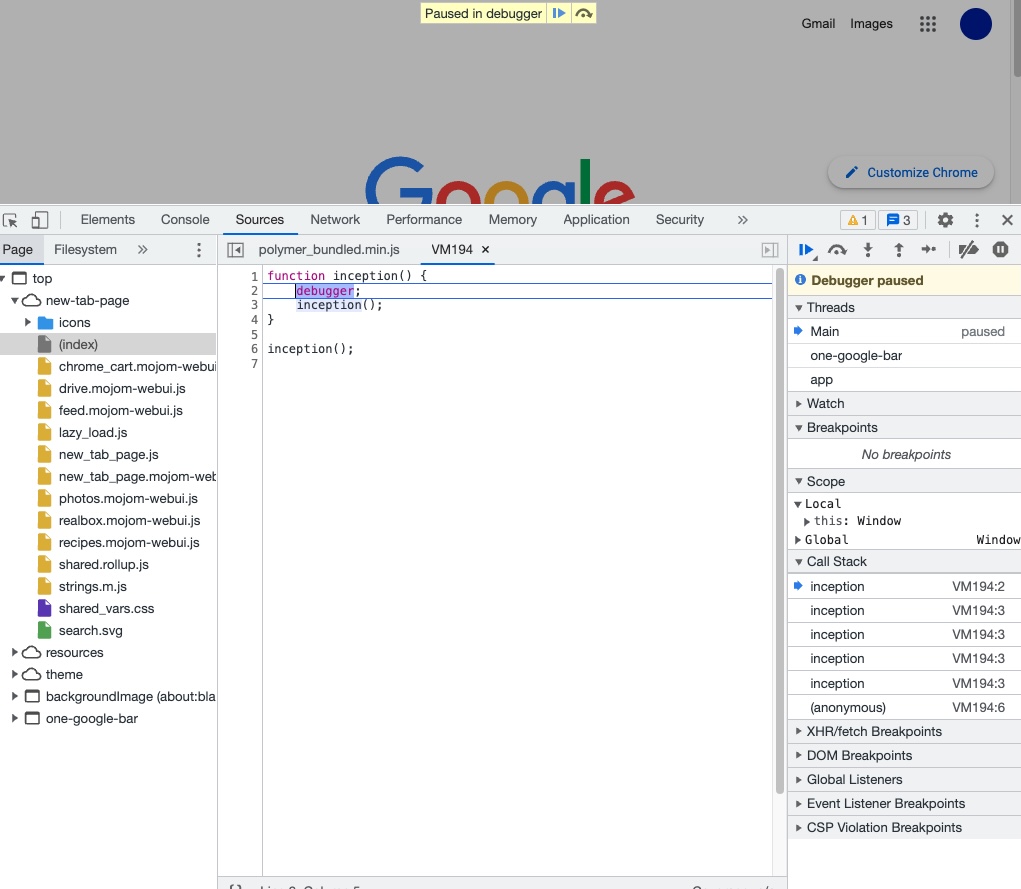
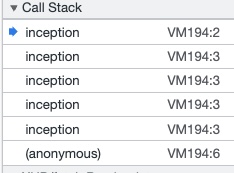
inception이 콜 스택의 제한된 메모리를 다 사용하면 결국 stack overflow가 발생한다.
156. Anatomy Of Recursion
What you need for recursion algorithm
- recursive case : how to recursive
- base case: how to quit recursion
Rule to create recursion
- Identify the base case. How you will quit?
- Identify the recursive case. ex) when counter is less than 10
- Get closer and closer and return when needed. Usually you have 2 returns(base case and recursive case).
How Recursion Works?
return하지 않는 inception()
| let counter = 0; function inception() { console.log(counter) if (counter > 3) { return 'done' } counter++; inception(); } console.log(inception()) //undefined |
This code returns undefined not ‘done’. Why?
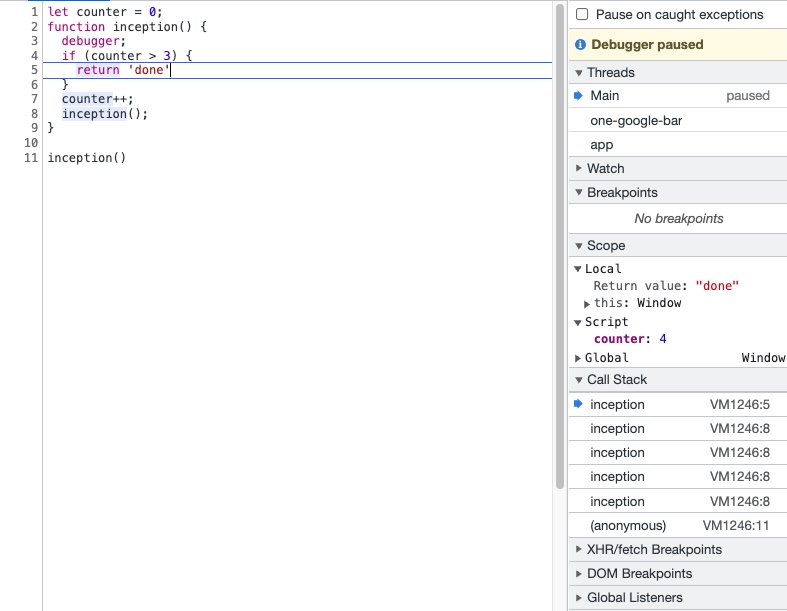
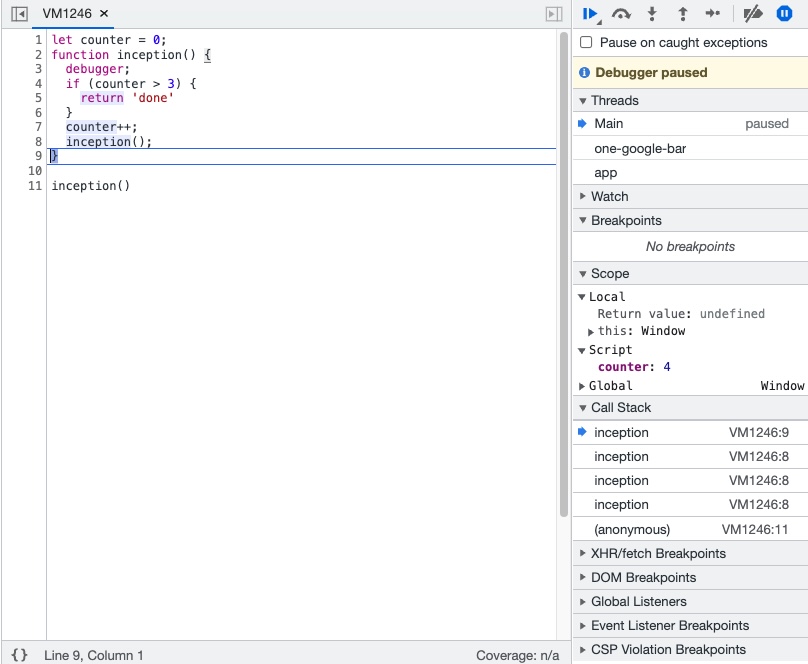
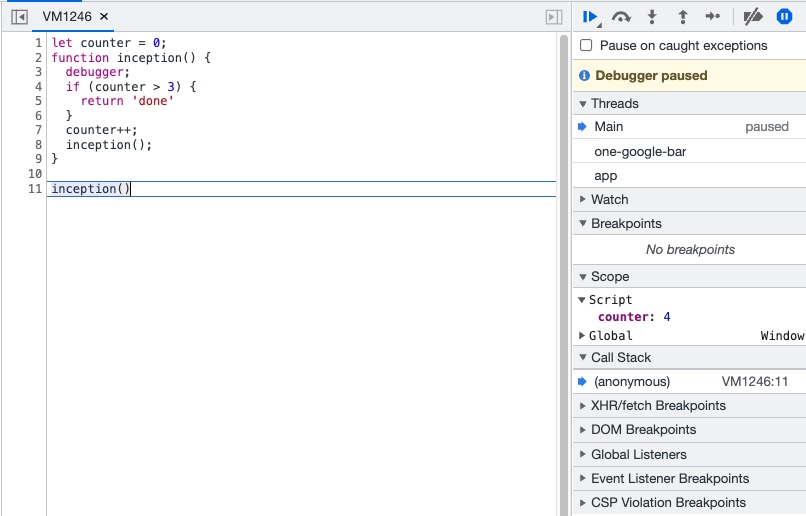
분명히 counter가 4이고 counter > 3 조건이 충족되었을 때 local scope에 return value “done”이 저장되었었다. 그러나 그 다음에는 Return value가 undefined로 바뀐다.
그리고 계속 넘기다 보면 결국 콜스택이 비워진다. 왜그런걸까? Recursive를 코드로 표현하면 이해가 편하다.
inception(inception(inception(inception(inception()))))
->
inception(inception(inception(inception(‘done’))))
inception()의 끝은 결국 ‘done’을 리턴하는데, 리턴된 ‘done’가 상위의 inception()의 매개변수로 들어가게 된다. inception은 매개변수를 다루지 않고 그 자체로 리턴하는 것이 없기 때문에 undefined를 리턴한다.
그래서 마지막에 return을 추가해줘야 한다.
return하는 inception()
| let counter = 0; function inception() { if (counter > 3) { return 'done' } counter++; return inception(); } console.log(inception()); // 'done' |
157. Exercise: Factorial
| // Write two functions that finds the factorial of any number. One should use recursive, the other should just use a for loop // O(n) function findFactorialRecursive(number) { if (number === 2) { return 2; } return number * findFactorialRecursive(number - 1); } // O(n) function findFactorialIterative(number) { let answer = 1; if (number === 2) { answer = 2; } for(let i = 2; i <= number; i++) { answer *= i } return answer; } console.log(findFactorialRecursive(5)); // console.log(findFactorialIterative(5)); |
Recursion 함수는 다시 Recursion 함수를 리턴한다. 이때 매개변수를 다음 Recursion 함수의 리턴값과 곱해주는데 이때 다음 Recursion 함수의 매개변수는 이전 함수보다 -1 낮은 함수를 대입해준다. 5 * (5-1) * (4-1) … 이렇게 진행이 되는 것이다. 그러다가 number가 2일 경우, 즉 Recursion이 아니라 2를 리턴하여 최종적으로 Recursion이 끝난다.
Recursion(5)
5 * Recursion(4)
5 * 4 * Recursion(3)
5 * 4 * 3 * Recursion(2)
5 * 4 * 3 * 2
120
159. Exercise: Fibonacci
fibonacciIterative code in O(n).
fibonacciRecursive code in O(2^n), exponential time.
Even though recursive is slower, why do we need to use this?
| // Given a number N return the index value of the Fibonacci sequence, where the sequence is: // 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 ... // the pattern of the sequence is that each value is the sum of the 2 previous values, that means that for N=5 → 2+3 //For example: fibonacciRecursive(6) should return 8 // O(n) function fibonacciIterative(n){ let arr = [0, 1]; for (let i = 2; i < n + 1; i++) { arr.push(arr[i-2] + arr[i-1]) } return arr[n] } console.log(fibonacciIterative(3)); // O(2^n) : Exponential time, recursive algorithms that solve a problem of size N function fibonacciRecursive(n) { if (n < 2) { return n; } return fibonacciRecursive(n-1) + fibonacciRecursive(n-2) } // console.log(fibonacciRecursive(0)) |

161. Recursive VS Iterative
“Anything you do with a recursion CAN be done iterative(loop)”
Recursion Pros and Cons
Pros
- keep code dry
- Readability
Cons
- Large Stack(memory)
Tail Call Optimization
Some languages provide tail call optimization. In JS, ES6 allows using recursion without making call stack
162. When Do I use Recursion?
Complicated Problem
In situation you don’t how deep the data structure is, you can use recursion for traversing in tree, graphs.
Rule
Every time you are using a tree or converting something into a tree, consider recursion
이런 유형의 문제를 만나면 Recursion을 고려해야 한다
- Divided into a number of subproblems that are smaller instances of the same problem
- Each instance of the subproblem is identical in nature
- The solutions of each subproblem can be combined to solve the problem at hand
Divide and Conquer using Recursion.
163. Exercise: Reverse String with Recursion
| function reverseString(str) { let arrayStr = str.split(""); let reversedArray = []; //We are using closure here so that we don't add the above variables to the global scope. function addToArray(array) { if(array.length > 0) { reversedArray.push(array.pop()); addToArray(array); } return; } addToArray(arrayStr); return reversedArray.join(""); } reverseString('yoyo master'); function reverseStringRecursive (str) { if (str === "") { return ""; } else { return reverseStringRecursive(str.substr(1)) + str.charAt(0); } } reverseStringRecursive('yoyo master'); |
164. Recursion Review
“Every time you are using a tree or converting something into a tree, consider recursion”
Recursion is not good for memory. But it makes code dry and readable.
'Research > Data structure & algorithm' 카테고리의 다른 글
| s15. Algorithm: Dynamic Programming (0) | 2022.12.03 |
|---|---|
| s13. Algorithm: DFS + DFS(Searching) (0) | 2022.12.03 |
| s11. Data Structure: Graphs (0) | 2022.11.30 |
| s10. Data Structure: Trees (0) | 2022.11.29 |
| Data Structure: Stacks + Queues (0) | 2022.11.28 |




댓글