126. Trees Introduction
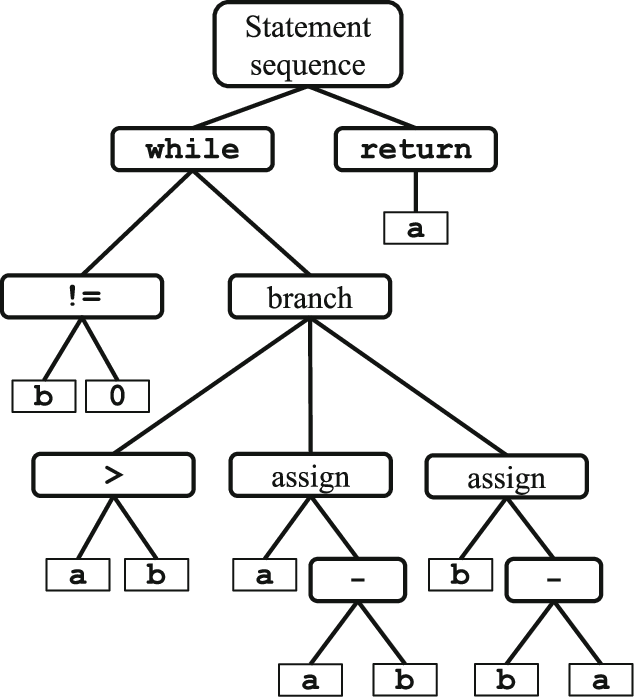
*Abstract Syntax tree
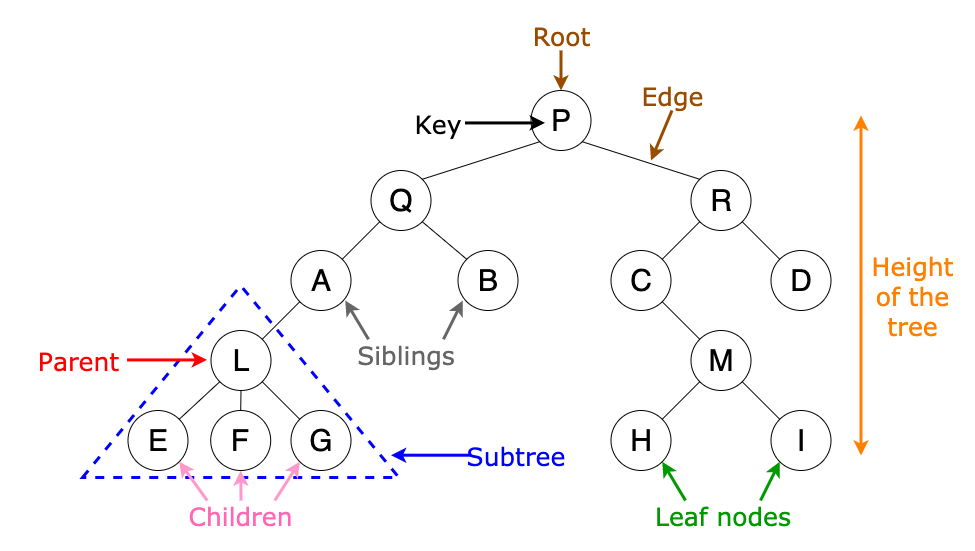
What is Tree data structure
- Trees have hierarchical structure. In contrast, array, linked lists, stacks, queue have linear structure.
- in tree data structure node can point only its child
트리 구조의 핵심은 1) 수직 구조이며 2)노드가 가리킬 수 있는 것은 노드의 자식 뿐이다. 수평 구조를 가진 다른 어레이, 링크드리스트, 스택, 큐 등과 차이점이다.
Element of Tree structure
- Root
- Parent
- Child
- Leaf
- Sibling
트리구조의 구성 요소는 크게 5개로 루트, 부모, 자식, 리프, 시블링 노드로 구분할 수 있다. 흥미로운 점은 상대적인 위치에 따라 구분되기 때문에 자식 노드가 어떤 노드의 부모 노드이기도 하다. 인간 족보 구조와 유사하다.
127. Binary Trees
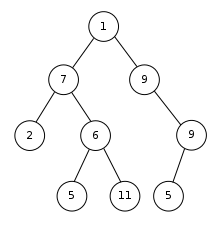
Rule of Binary Trees
- Each node can only have 0, 1, 2 nodes
- Each child only can have one parent
바이너리 트리, 이진 트리는 규칙이 있다. 각 노드가 0, 1, 2개의 노드를 가진다. 각 자식 노드들은 단 하나의 부모 노드만 가진다.
Perfect Binary Trees
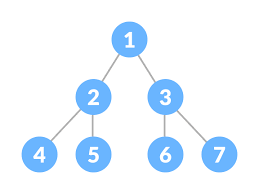
- node either has 2 or 0 childs
- all nodes are full
- Important properties
Big O
- lookup O(log N)
- insert O(log N)
- delete O(log N)
Full Binary Tree
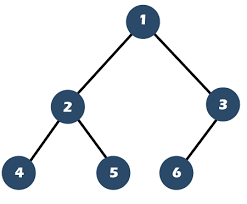
- node either has 2 or 0 childs
정리하자면, 바이너리 트리(이진트리)는 퍼펙트 트리와 풀 트리로 구분된다.
퍼펙트 트리는 노드가 0 또는 2개의 자식 노드를 가진다. 모든 노드는 가득 차있다. 이 구조가 가지는 중요한 프로퍼티는 2가지가 있는데, 1)위에서 아래 레이어로 내려갈 수록 개수가 2배로 커진다는 점과 2)가장 최하단의 레이어의 노드 개수가 그 나머지 상단부의 총 노드 개수 + 1개 노드 한 것과 동일하다는 점이다.
풀 바이너리 트리는 0 또는 2개 자식 노드를 가진다.
트리 구조는 기본적으로 divide and conquer 전략으로 데이터를 타게팅하는데 도움이 된다.
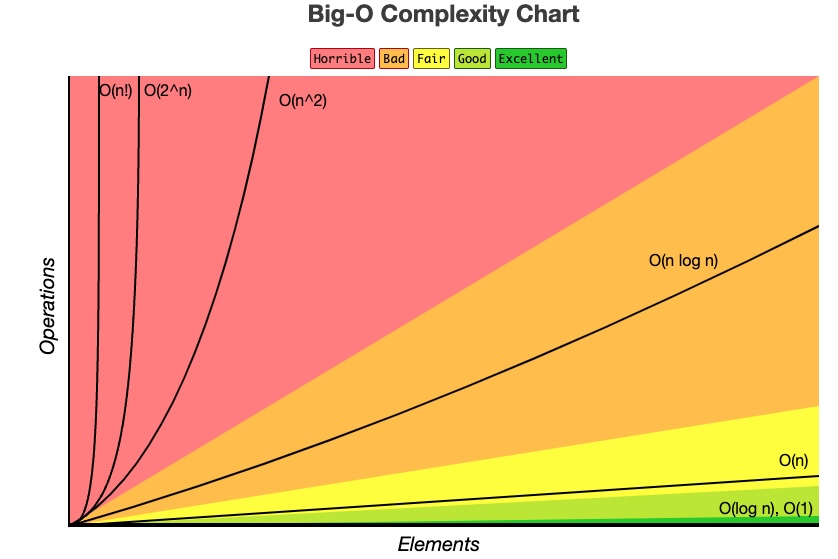
128. O(log n)
How to Measure
level 0: 2^0 = 1;
level 1: 2^1 = 2;
level 2: 2^2 = 4;
level 3: 2^3 = 8;
log 100 = 2
# of nodes = 2^steps- 1
log nodes = steps(maximum decision makings)
노드의 총 개수를 구하려면 2^층의 수에 -1을 해주면 된다. 만약 3개의 층이 있는 경우, 2^3-1이므로 총 7개 노드가 나온다. 사실 층은 0층부터 시작하므로 3개 층이 아니라 4층에서 1개를 빼준다는 느낌이 더 가깝다. 다른 방식으로 보려면 2^0 + 2^1 + 2^2, 즉 0층 + 1층 + 2층을 모두 더해주면 동일하게 7개 노드가 나온다는 것을 알 수 있다.
BigO
- lookup: O(log N)
- insert: O(log N)
- delete: O(log N)
| methods | Arrays | Hash Tables | Linked List | Stacks | Queue | Binary search Tree |
| search | O(n) | O(1) | ||||
| lookup | O(1) | O(1) or O(n) | O(n) | O(n) | O(n) | O(logN) |
| insert | O(n) | O(1) | O(n) | O(logN) | ||
| delete | O(n) | O(1) | O(n) | O(logN) | ||
| push | O(1) | O(1) | ||||
| prepend | O(1) | |||||
| append | O(1) | |||||
| pop | O(1) | |||||
| peek | O(1) | O(1) | ||||
| enqueue | O(1) | |||||
| dequeue | O(1) | |||||
| features | ||||||
| in order | yes | no | yes |
Binary Search Tree는 매우 효율적인 데이터 구조다.
129. Binary Search Tree
Pros
- very fast to searching and lookup
Rules
- All childs in the right tree must be greater than left
- Node can only can have up to 2 child nodes
바이너리 서치 트리, 이진 탐색 트리는 데이터를 찾고 둘러보는 것이 매우 빠르다. 구글 검색 엔진에서 이를 사용한다고 한다.
바이너리 서치 트리는 2개의 조건이 있는데, 1) 우측의 모든 노드들이 왼쪽의 노드보다 큰 숫자이며, 2) 노드는 최대 2개의 자식 노드를 가질 수 있다.
재미있는 점은 숫자를 어떤 순서로 넣냐에 따라 트리의 구조의 형태가 달라진다는 점이다. 변화에 순응하는 자연물같이 느껴져서 흥미롭다. 정보의 우연성에 따라 형태가 달라지는 트리의 성질을 이용하여 작품 하나를 만들면 재미있겠다는 생각이 든다.
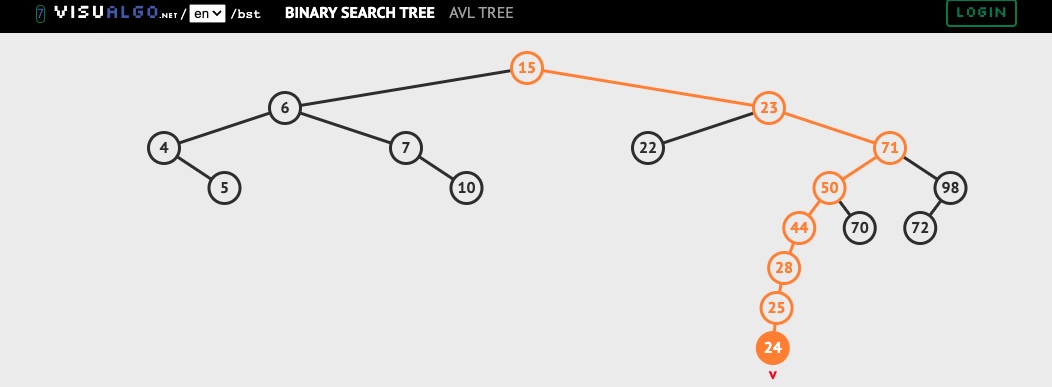
130. Balanced VS Unbalanced BST
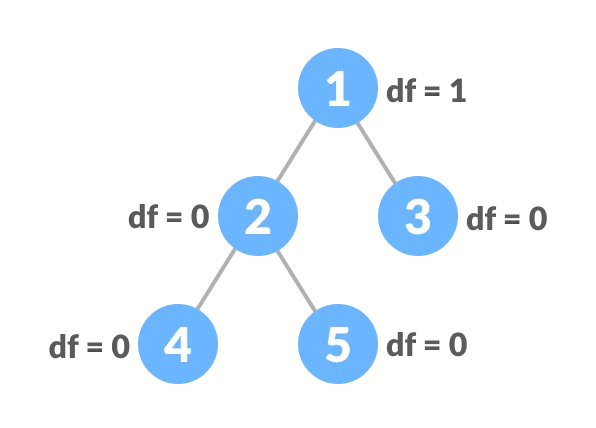
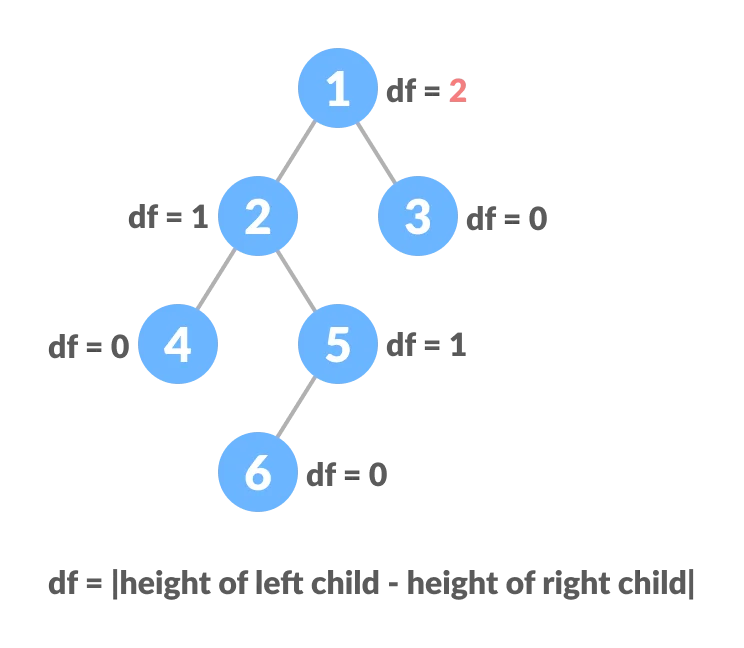
Interview Question: Why unbalanced BST is worse than balanced one?
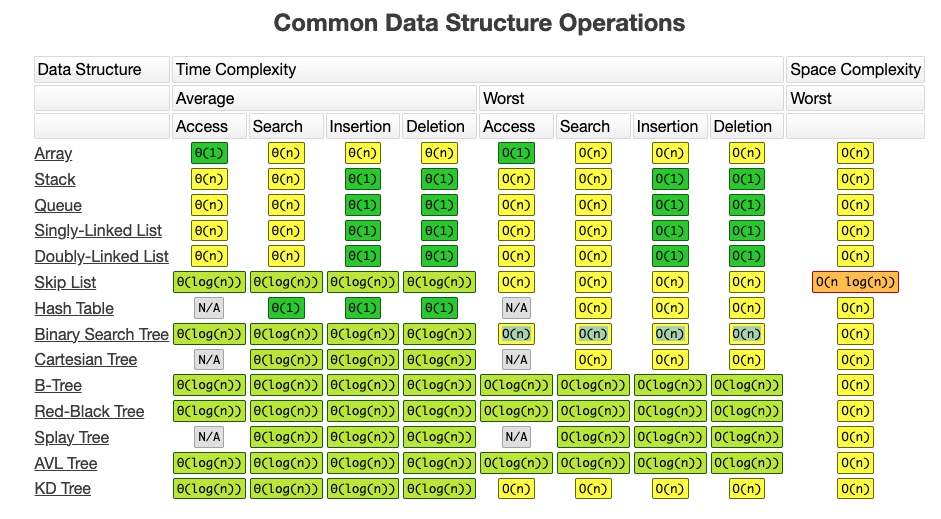
Because it’s O(n).
131. BST Pros and Cons
Binary Search Trees
Pros
- Better than O(n)
- Ordered
- Flexible Size
Cons
- No O(1) operations
In case of BST, lookup, insert, deletion can be faster than array. But BST does not have constant time like hash table.
To summarize, BST has fast average performance but it is not the fastest one.
132. Exercise: Binary Search Tree
| class Node { constructor(value) { this.left = null; this.right = null; this.value = value; } } class BinarySearchTree { constructor() { this.root = null; } insert(value) { const newNode = new Node(value); if (this.root === null) { this.root = newNode; } else { let currentNode = this.root; while (true) { if (value < currentNode.value) { //Left if (!currentNode.left) { currentNode.left = newNode; return this; } currentNode = currentNode.left; } else { //Right if (!currentNode.right) { currentNode.right = newNode; return this; } currentNode = currentNode.right; } } } } lookup(value) { if (!this.root) { return false; } let currentNode = this.root; while (currentNode) { if (value < currentNode.value) { currentNode = currentNode.left; } else if (value > currentNode.value) { currentNode = currentNode.right; } else if (currentNode.value === value) { return currentNode; } } return null; } remove(value) { if (!this.root) { return false; } let currentNode = this.root; let parentNode = null; while (currentNode) { if (value < currentNode.value) { parentNode = currentNode; currentNode = currentNode.left; } else if (value > currentNode.value) { parentNode = currentNode; currentNode = currentNode.right; } else if (currentNode.value === value) { //We have a match, get to work! //Option 1: No right child: if (currentNode.right === null) { if (parentNode === null) { this.root = currentNode.left; } else { //if parent > current value, make current left child a child of parent if (currentNode.value < parentNode.value) { parentNode.left = currentNode.left; //if parent < current value, make left child a right child of parent } else if (currentNode.value > parentNode.value) { parentNode.right = currentNode.left; } } //Option 2: Right child which doesnt have a left child } else if (currentNode.right.left === null) { currentNode.right.left = currentNode.left; if (parentNode === null) { this.root = currentNode.right; } else { //if parent > current, make right child of the left the parent if (currentNode.value < parentNode.value) { parentNode.left = currentNode.right; //if parent < current, make right child a right child of the parent } else if (currentNode.value > parentNode.value) { parentNode.right = currentNode.right; } } //Option 3: Right child that has a left child } else { //find the Right child's left most child let leftmost = currentNode.right.left; let leftmostParent = currentNode.right; while (leftmost.left !== null) { leftmostParent = leftmost; leftmost = leftmost.left; } //Parent's left subtree is now leftmost's right subtree leftmostParent.left = leftmost.right; leftmost.left = currentNode.left; leftmost.right = currentNode.right; if (parentNode === null) { this.root = leftmost; } else { if (currentNode.value < parentNode.value) { parentNode.left = leftmost; } else if (currentNode.value > parentNode.value) { parentNode.right = leftmost; } } } return true; } } } } const tree = new BinarySearchTree(); tree.insert(9); tree.insert(4); tree.insert(6); tree.insert(20); tree.insert(170); tree.insert(15); tree.insert(1); tree.remove(170); JSON.stringify(traverse(tree.root)); // 9 // 4 20 //1 6 15 170 function traverse(node) { const tree = { value: node.value }; tree.left = node.left === null ? null : traverse(node.left); tree.right = node.right === null ? null : traverse(node.right); return tree; } |
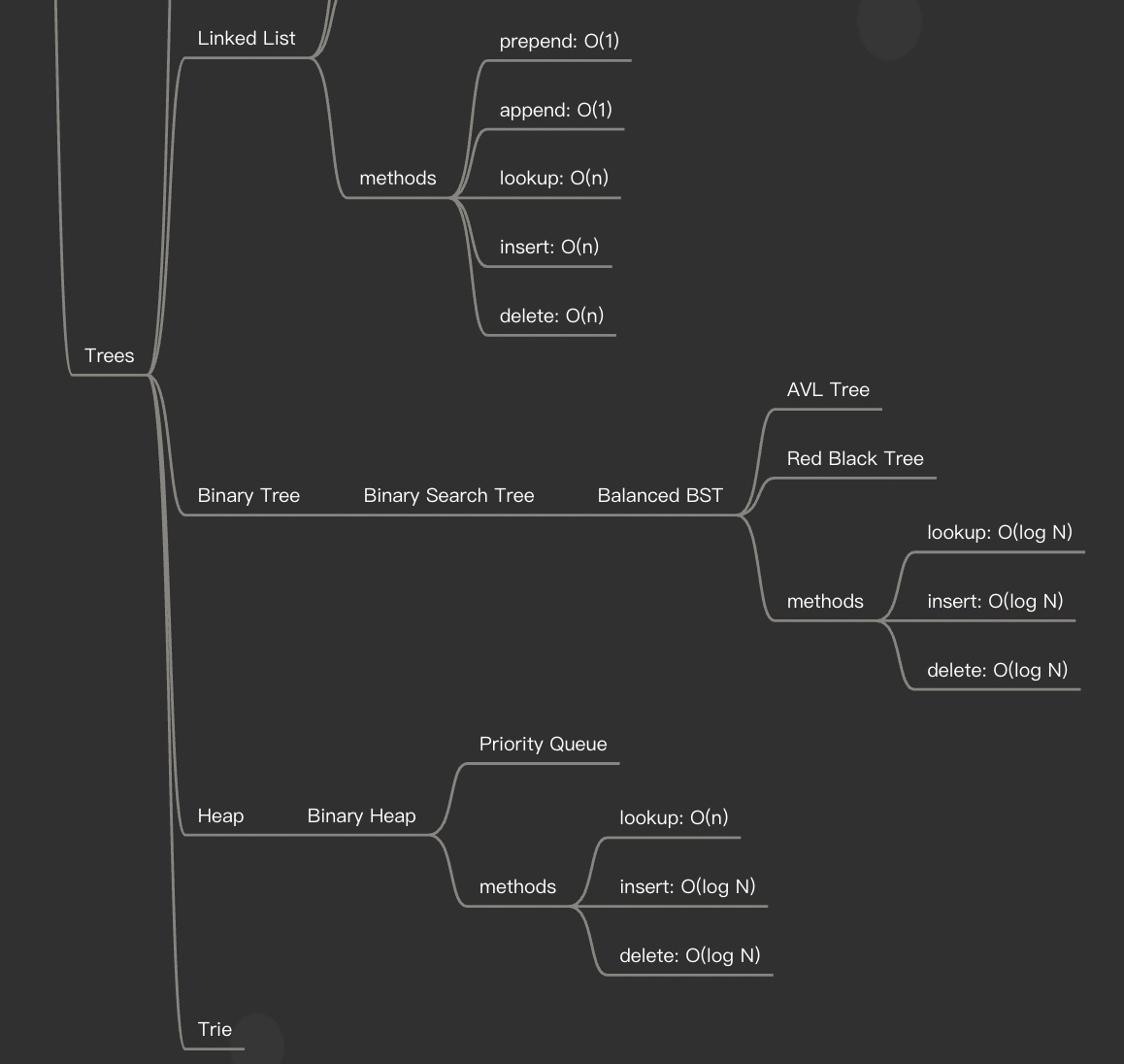
137. AVL Trees + Red Black Trees
There are two types of Balanced BST, 1) AVL Tree and 2)Red Black Tree.
What is AVL Trees?
The name of AVL trees came from its inventor Georgy Adelson-Velsky and Landis.
Balance factor of a node is an AVL tree is the difference between the height of the left subtree and that of the right subtree of that node.
Balance Factor = (Height of Left Subtree - Height of Right Subtree)
The self balancing property of an AVL tree is maintained by the balanced factor. The value of balance factor should always be -1, 0, or +1.
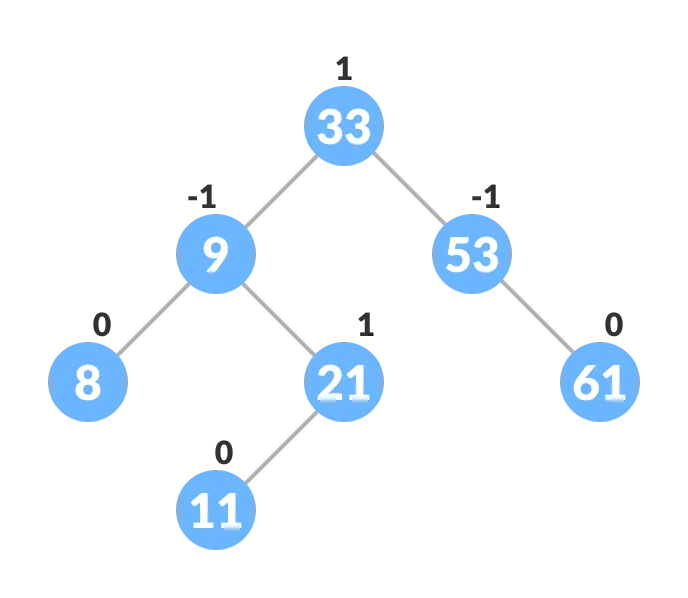
https://www.programiz.com/dsa/avl-tree
What is Red Black Tree?
It is invented by Rudolf Bayer in 1972.
A red-black tree is a kind of self-balancing binary search tree where each node has an extra bit, and that bit is often interpreted as the color red or black. These colors are used to make sure that the tree is balanced during insertions and deletions. It is useful to save the searching time and maintain it around O(log n) time, where n is the total number of elements in the tree.
Each node requires only 1 bit of space to store the color information, these types of trees show identical memory footprints to the classic binary search tree.
Rule
- Every node has a color either red or black
- The root of the tree is always black
- There are no two connected red nodes
- Every path from a node to any of its descendants NULL nodes has the same number of black nodes
- All leaf nodes are black nodes
AVL Tree vs. Red/Black Tree
Generally, the AVL trees are more balanced compared to Red-Black Trees.
- frequent insertions and elections? Red-Black tree
- frequent search? AVL tree
https://medium.com/basecs/the-little-avl-tree-that-could-86a3cae410c7
https://medium.com/basecs/painting-nodes-black-with-red-black-trees-60eacb2be9a5
https://www.cs.usfca.edu/~galles/visualization/AVLtree.html
https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
https://www.geeksforgeeks.org/introduction-to-red-black-tree/
139. Binary Heaps
Heap, Trie
Binary Heap types
- Max heap: Parent is bigger than childs
- Min heap: Parents are smaller than childs. The root is the smallest one.
Big O
- lookup: O(n)
- insert: O(log N) - in case of best O(1)
- delete: O(log N)
Pros
- Better than O(n)
- Priority
- Flexible Size
- Fast Insert(if high priority)
Cons
- Slow lookup
Why we use this?
- It is very good for comparative operation
- We use this where its order matters. Heap manipulate the positions if order should be changed.
140. Quick Note on Heaps
Memory Heap != Heap Data Structure
Memory Heap in JS runtime engine is not the Heap Data Structure!!
141. Priority Queue
There is no unbalanced concept in Binary Heap because we don’t need this.
Binary Heap is good for ‘Priority Queue’
Priority queue means each elements have priority. For e.g., VIP comes first in Club’s queue or emergency rooms in hospital.
VIPs 리스트 기반하여 누가 누구에게 먼저 우선권을 줄 것인지 알고리즘 만들어볼 것
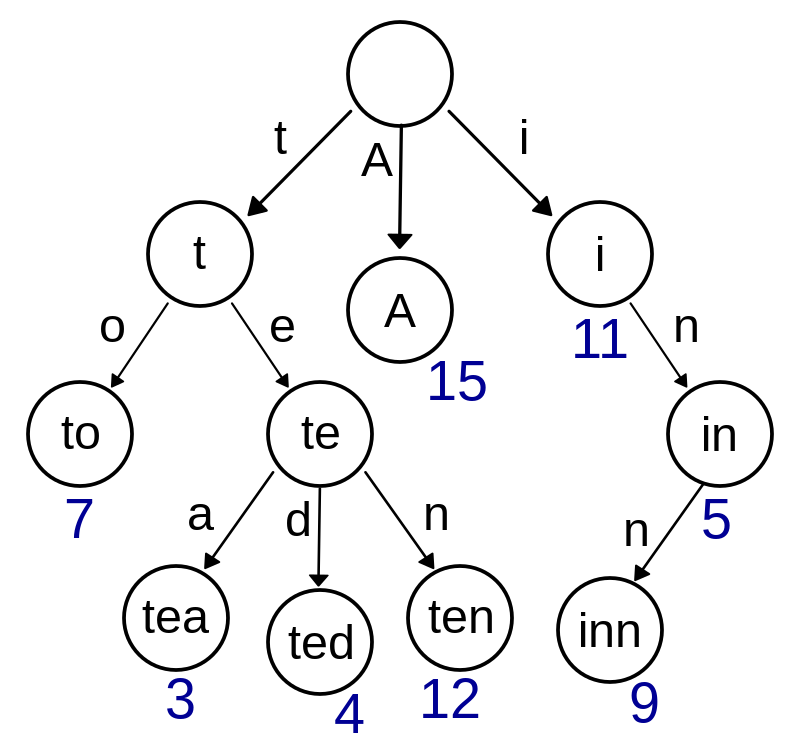
142. Trie
What is Trie?
Specialized tree for searching by text.
root node is normally empty.
root children are multiples.
Good for
- dictionary. n? news or not
- Auto suggestion
- IP routing
흥미롭다. 루트에서 뻗어져 나온 뒤 처음 찾는 인덱스에서 파생된 정보들을 훑는 구조를 가지고 있다. 이것을 시각 정보에 적용하면 어떻게 될까? 만약 ‘자켓' 실루엣이 있다면 그 다음은 ‘자켓’의 컬러와 길이를 체크하고 그 다음 컬러에서 또 세부적으로 구분하며 찾고.. 이미지 정보를 Trie 적용할 수 있을지는 모르겠지만.
Big O
- O(length of word)
'Research > Data structure & algorithm' 카테고리의 다른 글
| s12. Algorithm: Recursion (0) | 2022.12.01 |
|---|---|
| s11. Data Structure: Graphs (0) | 2022.11.30 |
| Data Structure: Stacks + Queues (0) | 2022.11.28 |
| Data Structure: Hash Tables (0) | 2022.11.25 |
| Data Structure: Arrays (0) | 2022.11.24 |




댓글