What is Graphs?
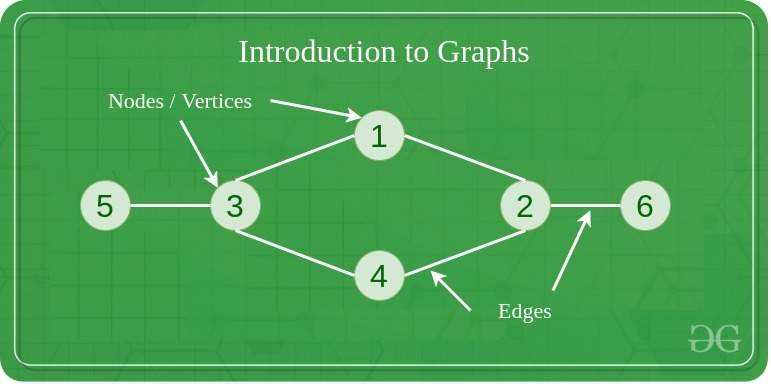
A graph is a non-linear data structure consisting of vertices and edges.
- node(=vertex)
- edge : lines or arcs connecting two nodes
The graph is denoted by G(E, V).
Graphs are useful for modeling real life such as shortest-path guid(Google maps), social network(Facebook), recommendation engine(Amazon) etc.
그래프는 비선형적 데이터 구조 중 하나로 노드(벌텍스)들과 엣지들로 구성된다. 여기서 엣지는 두 노드를 연결하는 선을 의미한다.
Pros and cons
Pros
- very good for expressing relationships
Cons
- Scaling is hard
145. Types Of Graphs
Undirected and Undirected
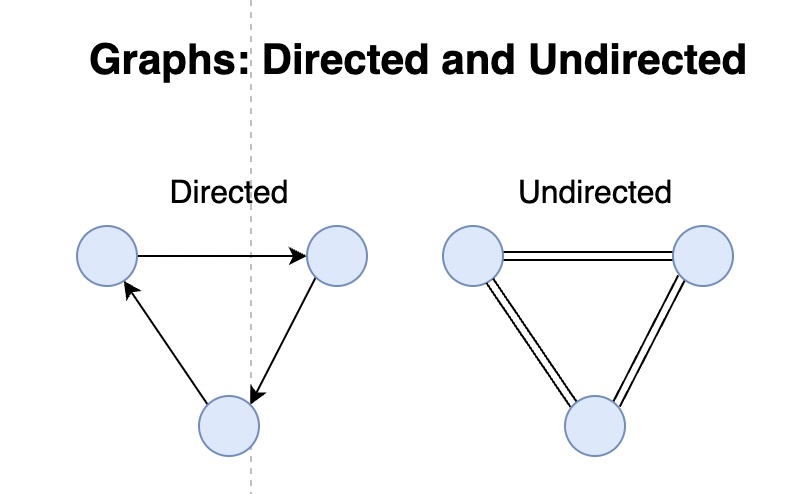
Examples
- Both are : traffic flow
Weighted Graph
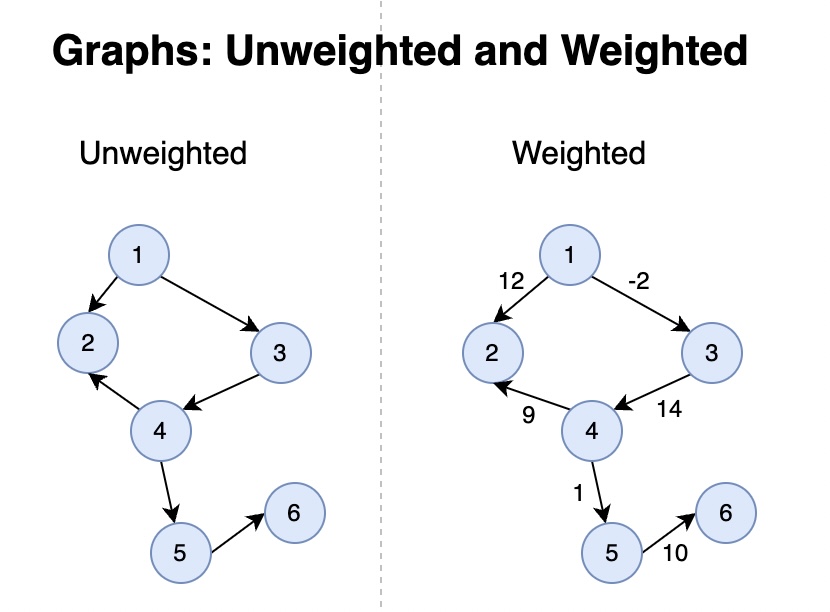
Values can be applied in various aspects of graphs.
You can score its way. What is shortest path?
Cyclic Graph
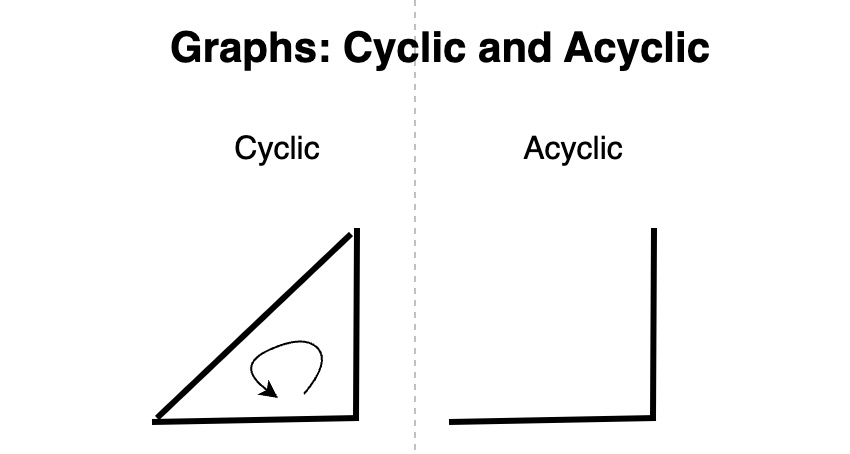
useful for google map checking its way to get back.
그래프의 유형은 3가지 기준에서 분류할 수 있다. 1) 노드의 방향, 2)무게 그리고 3) 순환 여부다. 노드의 라인의 하나의 방향으로만 가르키는 경우 directed, 양쪽 모두 가르키면 undirected라고 한다. 노드 사이의 그 라인을 값으로 평가할 수 있는 경우 weigthed, 그렇지 않으면 unweighted라 한다. 최단거리를 계산하기 위해 노드 간 엣지의 점수를 매길 때 사용한다고 한다. 세번 째는 그 그래프가 순환 가능하냐의 여부이다. 순환 한다면 Cyclic이고 그렇지 않으면 Acyclic이라 한다.
146. Exercise: Guess The Graph
https://visualgo.net/en/graphds
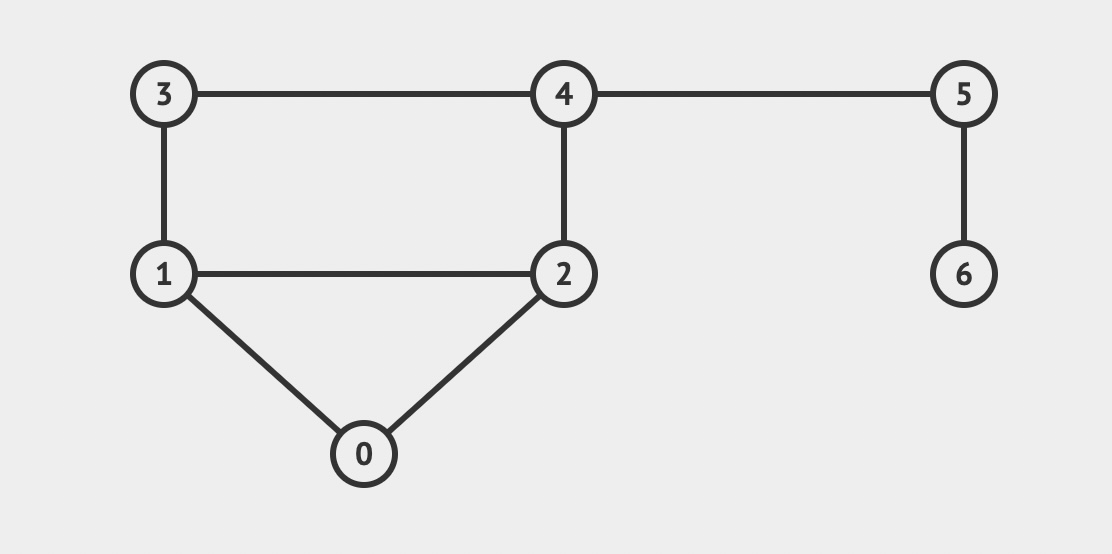
- undirected
- unweighted
- cyclic
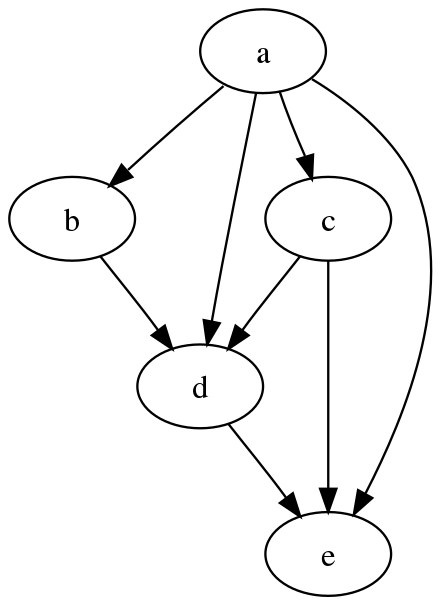
Directed Acyclic Graph(DAG)
- popular graph type
- this can be created based on tree and linkedList
그래프의 대표적인 유형으로 Directed Acyclic Graph(DAG)가 있다. 그래프마다 다른 특징이 있기 때문에 위 3가지 기준으로 평가를 하면 그래프를 비교하는데 도움을 줄 것이다.
147. Graph Data
How to make graph with code?
| // Edge List const graph = [[0, 2], [2, 3], [2, 1], [1, 3]] // Adjacent List // - index of the array is the value of the actual Graph node. Object useful for this const graph = [[2], [2,3], [0, 1, 3], [1, 3]] or in object .. // Adjacent Matrix // 0 - no, 1 - yes const graph = { 0: [0, 0, 1, 0], // node 0 is connected to 2 1: [0, 0, 1, 1], // node 1 is connected to 2, 3 2: [1, 1, 0, 1], // node 2 is connected to 0, 1, 2 3: [0, 1, 1, 0] // node 3 is connected to 1, 2 } |
148. Exercise: Graph Implementation
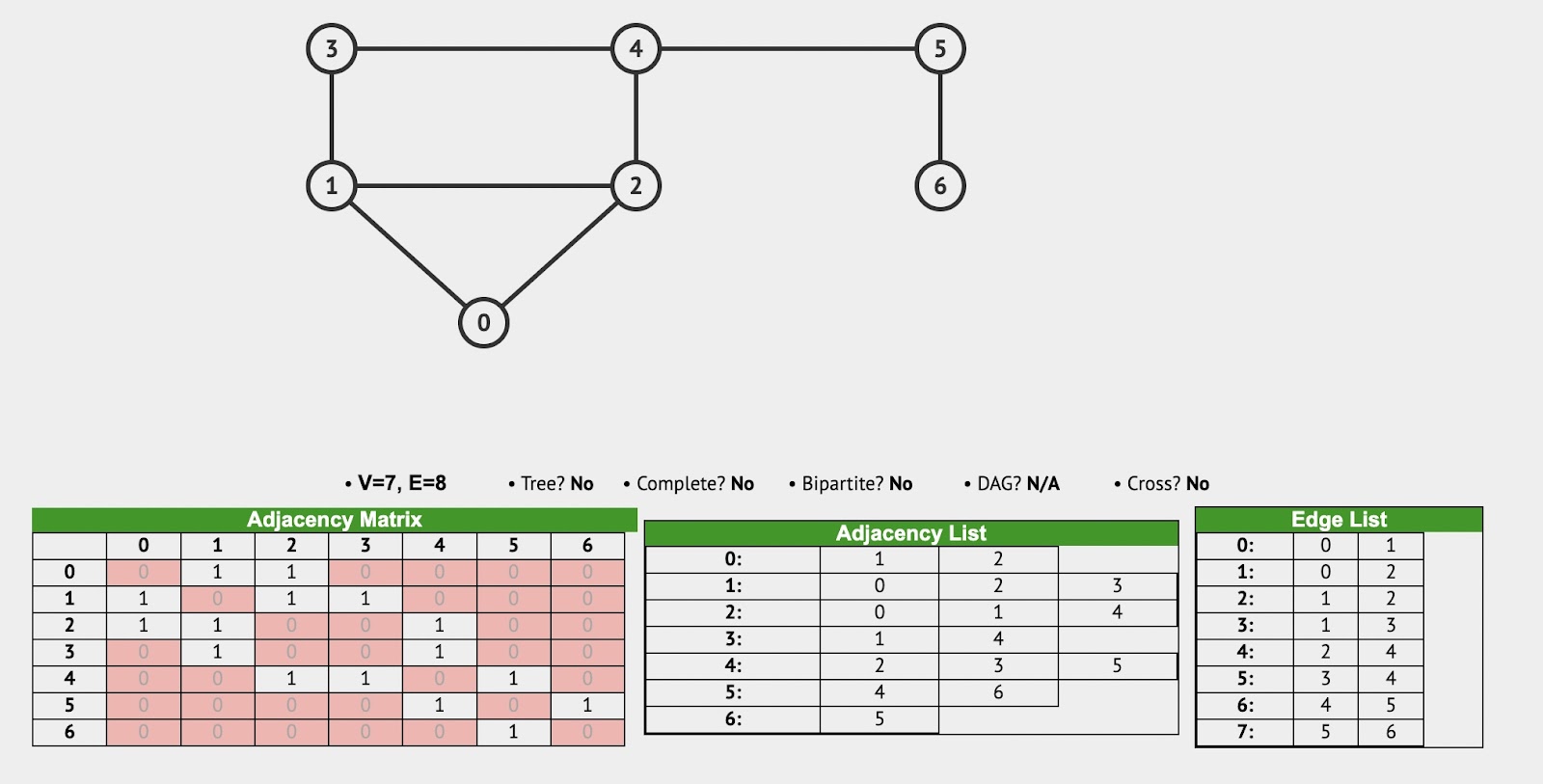
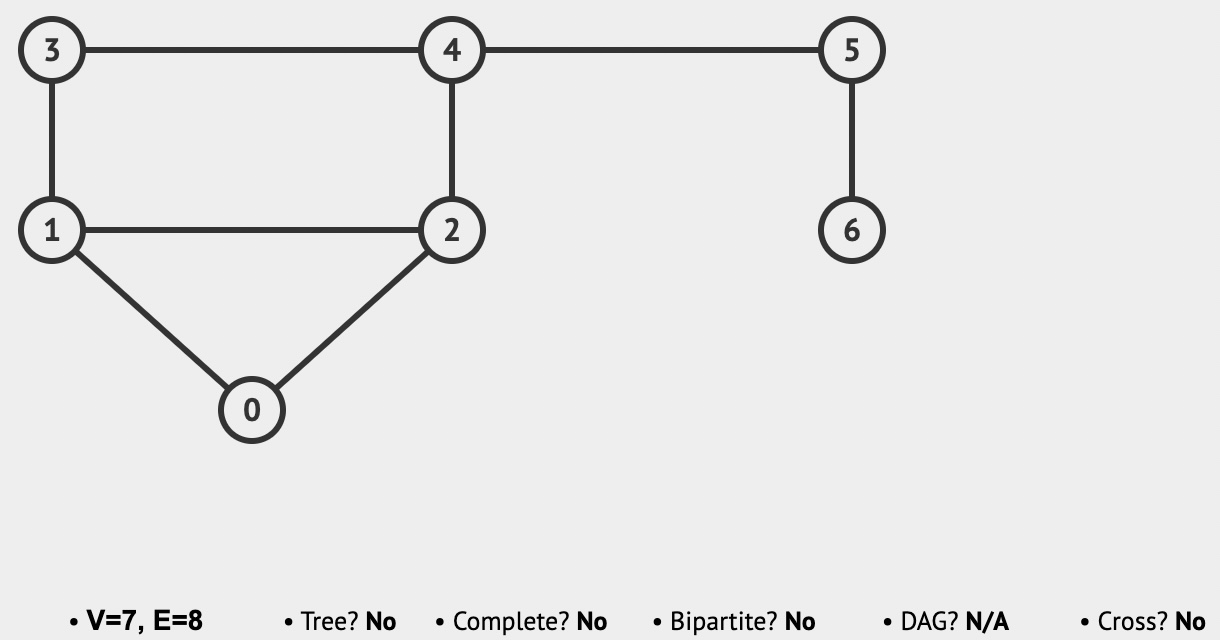
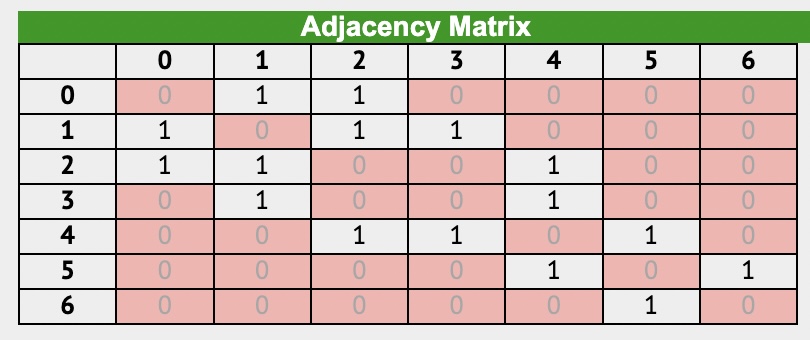
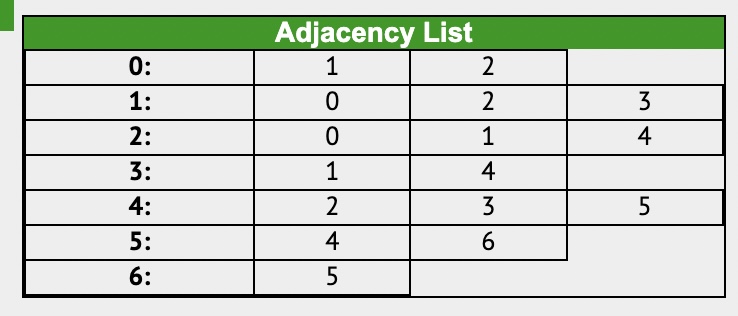
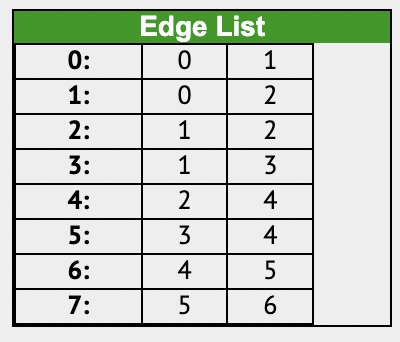
| class Graph { constructor() { this.numberOfNodes = 0; this.adjacentList = { }; } addVertex(node) { this.adjacentList[node] = []; this.numberOfNodes++; // if(!this.adjacentList[node]) { // this.adjacentList[node] = []; // } // this.numberOfNodes++ } addEdge(node1, node2) { // undirected Graph this.adjacentList[node1].push(node2); this.adjacentList[node2].push(node1); // if (!this.adjacentList[node1].includes(node2)){ // this.adjacentList[node1].push(node2) // } // if (!this.adjacentList[node2].includes(node1)){ // this.adjacentList[node2].push(node1) // } } showConnections() { const allNodes = Object.keys(this.adjacentList); for (let node of allNodes) { let nodeConnections = this.adjacentList[node]; let connections = ""; let vertex; for (vertex of nodeConnections) { connections += vertex + " "; } console.log(node + "-->" + connections); } } } const myGraph = new Graph(); myGraph.addVertex('0'); myGraph.addVertex('1'); myGraph.addVertex('2'); myGraph.addVertex('3'); myGraph.addVertex('4'); myGraph.addVertex('5'); myGraph.addVertex('6'); myGraph.addEdge('3', '1'); myGraph.addEdge('3', '4'); myGraph.addEdge('4', '2'); myGraph.addEdge('4', '5'); myGraph.addEdge('1', '2'); myGraph.addEdge('1', '0'); myGraph.addEdge('0', '2'); myGraph.addEdge('6', '5'); myGraph.showConnections(); //Answer: // 0-->1 2 // 1-->3 2 0 // 2-->4 1 0 // 3-->1 4 // 4-->3 2 5 // 5-->4 6 // 6-->5 |
'Research > Data structure & algorithm' 카테고리의 다른 글
| s13. Algorithm: DFS + DFS(Searching) (0) | 2022.12.03 |
|---|---|
| s12. Algorithm: Recursion (0) | 2022.12.01 |
| s10. Data Structure: Trees (0) | 2022.11.29 |
| Data Structure: Stacks + Queues (0) | 2022.11.28 |
| Data Structure: Hash Tables (0) | 2022.11.25 |




댓글