212. Dynamic Programming Introduction
Dynamic programming is an optimization technique. If you have something you can cache, just do Dynamic Programming.
Caching? -> Dynamic Programming
213. Memoization 1
What is Caching?
Storage. Caching is the way to store value to use later on.
holding datas you need -> speed up prgram by holding something.
Memoization is specific form of caching that involves caching the return value.
Before Implement caching
| function addTo80(n) { console.log('long time') return n + 80; } console.log(addTo80(5)); console.log(addTo80(5)); |
Implementing caching
| function addTo80(n) { console.log('long time') return n + 80; } let cache = { }; function memoizedAddTo80(n) { // If sth exist in cache if (n in cache) { return cache[n]; } else { console.log('long time..') cache[n] = n + 80; return cache[n]; } } console.log(memoizedAddTo80(5)) console.log(memoizedAddTo80(5)) |
214. Memoization 2
If we don’t want to create global variable such as let cache = {};?
For this, you can use closure in Javascript.
| function addTo80(n) { console.log('long time') return n + 80; } // With closure, you can avoid global scope vars function memoizedAddTo80(n) { let cache = {}; return function(n) { if (n in cache) { return cache[n]; } else { console.log('long time..') cache[n] = n + 80; return cache[n]; } } } const memoized = memoizedAddTo80(); console.log(memoized(5)) // 85 console.log(memoized(6)) // 86 console.log(memoized(5)) // 85, cached |
215. Fibonacci and Dynamic Programming
| let calculations = 0; function fibonacci(n) { calculations++; if (n < 2) { return n } return fibonacci(n-1) + fibonacci(n-2); } console.log(fibonacci(10)) console.log(calculations) |
This Fibonacci function has O(2^n) Big O. But with Dynamic Programming, you can convert O(2^n) into O(n). Wow.
216. Dynamic Programming
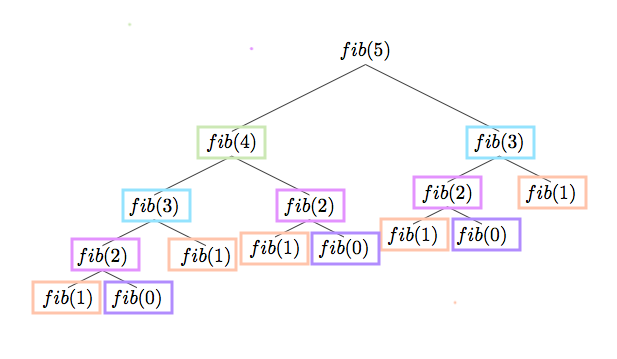
Fibonacci consists of bunch of repeated works. With Dynamic Programming, you can optimize by caching datas. Once you calculated formula, you don’t have to repeat again and just ask memoization what is the return.
Dynamic Programming
Dynamic Programming = Divide & Conquer + Memoization(re-use with caching)
Dynamic Programming Implementation Process
- Can it be divided into subproblems? -> indicating recursion solution
- -> Apply Recursive Solution
- Are there repetitive subproblems?
- -> Apply Memoize subproblems
- Demand a raise from your boss ;D. because you save calculations in terms of time complexity.
217. Implementing Dynamic Programming
| // Normal fibonacci let calc_fibo = 0; function fibonacci(n) { calc_fibo++; if (n < 2) { return n } return fibonacci(n-1) + fibonacci(n-2); } // Normal fibonacci in Dynamic Programming let calc_dp = 0; function fibonacciMaster() { let cache = {}; // Closure return function fib(n) { calc_dp++; if (n in cache) { return cache[n]; } else { if (n < 2) { return n; } else { cache[n] = fib(n-1) + fib(n-2); return cache[n]; } } } } const fasterFib = fibonacciMaster(); console.log('Normal', fibonacci(10), ':', calc_fibo); console.log('DP', fasterFib(10), ':', calc_dp); // Normal 55 : 177 // DP 55 : 19 |
일반 피보나치는 incremental 작업을 177회나 수행하는 반면 Dynamic Programming의 Caching 을 사용한 경우 19회밖에 수행하지 않는다. 왜냐하면 이미 caching에 저장을 해두었기 때문이다.
기존 피보나치의 O(2^n)이었는데, DP는 Time Complexity는 O(n)으로 시간 복잡도를 줄일 수 있다. 하지만 피보나치 계산의 개수만큼 Space Complexity는 늘어난다는 이슈가 있다.
219. Interview Questions: Dynamic Programming
Here are some popular Dynamic Programming Questions (see if you can notice the pattern):
https://leetcode.com/problems/house-robber/
https://leetcode.com/problems/best-time-to-buy-and-sell-stock/
https://leetcode.com/problems/climbing-stairs/
220. Dynamic Programming Review
Another way bottom up
| // DP bottom up function fibonacciMaster2(n) { let answer = [0, 1]; for (let i = 2; i <= n; i++) { answer.push(answer[i-2] + answer[i-1]); } return answer.pop(); } console.log(fibonacciMaster2(20)) |
'Research > Data structure & algorithm' 카테고리의 다른 글
| 시간복잡도와 공간복잡도 (0) | 2023.03.18 |
|---|---|
| 01. Array 배열의 정의와 구현(JS) (0) | 2023.02.05 |
| s13. Algorithm: DFS + DFS(Searching) (0) | 2022.12.03 |
| s12. Algorithm: Recursion (0) | 2022.12.01 |
| s11. Data Structure: Graphs (0) | 2022.11.30 |


댓글